问题
解答题
| 已知:如图,△ABC中,∠ABC=45°,DH垂直平分BC交AB于点D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F. (1)求证:BF=AC; (2)求证:CE=
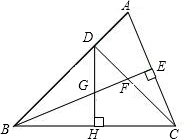 |
答案
证明:(1)∵DH垂直平分BC,且∠ABC=45°,
∴BD=DC,且∠BDC=90°,
∵∠A+∠ABF=90°,∠A+∠ACD=90°,
∴∠ABF=∠ACD,
∴△BDF≌△CDA,
∴BF=AC.
(2)由(1)得BF=AC,
∵BE平分∠ABC,且BE⊥AC,
∴在△ABE和△CBE中,
,∠ABE=∠CBE BE=BE ∠AEB=∠CEB=90°
∴△ABE≌△CBE(ASA),
∴CE=AE=
AC=1 2
BF.1 2
