问题
解答题
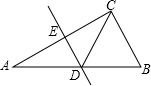
（1）已知：如图RT△ABC中，∠ACB=90°，ED垂直平分AC交AB与D，求证：DA=DB=DC．
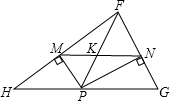
（2）利用上面小题的结论，继续研究：如图，点P是△FHG的边HG上的一个动点，PM⊥FH于M，PN⊥FG于N，FP与MN交于点K．当P运动到某处时，MN与FP正好互相垂直，请问此时FP平分∠HFG吗？请说明理由．
答案
（1）∵ED垂直平分AC，
∴AD=CD，
∴∠A=∠ACD，
∵∠ACB=90°，
∴∠A+∠B=∠ACD+∠BCD=90°，
∴∠B=∠BCD，
∴BD=CD，
∴DA=DB=DC；
（2）如图，作线段MF的垂直平分线交FP于点O，
∵PM⊥FH，PN⊥FG，
∴△MPF和△NPF都是直角三角形；
作线段MF的垂直平分线交FP于点O，
由（1）中所证可知OF=OP=OM；
作线段FN的垂直平分线也必与FP交于点O；
∴OM=OP=OF=ON，
又∵MN⊥FP，
∴∠OKM=∠OKN=90°，
∵OK=OK；
∴Rt△OKM≌Rt△OKN；
∴MK=NK；
∴△FKM≌△FKN；
∴∠MFK=∠NFK，
即FP平分∠HFG．