问题
解答题
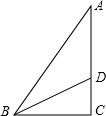
如图所示，在△ABC中，∠A=30°，∠C=90°，BD是∠ABC的平分线，交AC于点D．求证：点D在线段AB的垂直平分线上．
答案
证明：∵∠C=90°，∠A=30°，
∴∠ABC=60°．
∵BD平分∠ABC，
∴∠ABD=
∠ABC=1 2
×60°=30°．1 2
∴∠A=∠ABD，
∴DA=DB．
∴点D在AB的垂直平分线上．
搜题请搜索小程序“爱下问搜题”
如图所示，在△ABC中，∠A=30°，∠C=90°，BD是∠ABC的平分线，交AC于点D．求证：点D在线段AB的垂直平分线上．
证明：∵∠C=90°，∠A=30°，
∴∠ABC=60°．
∵BD平分∠ABC，
∴∠ABD=
∠ABC=1 2
×60°=30°．1 2
∴∠A=∠ABD，
∴DA=DB．
∴点D在AB的垂直平分线上．