问题
解答题
已知函数f(x)=
(1)判断函数f(x)的奇偶性,并证明; (2)求证函数f(x)在x∈(-∞,+∞)上是增函数. |
答案
由题意知:
(1)f(x)是奇函数.
证明:∵对∀x∈R
有f(-x)=
=2-x-1 2-x+1
=(2-x-1)2x (2-x+1)2x
=-f(x)1-2x 1+2x
∴根据奇函数的定义可知:f(x)是奇函数
(2)任取x1,x2∈R,设x1<x2
则f(x1)-f(x2)=
-2x1-1 2x1+1
=2x2-1 2x2+1
=(2x1-1)(2x2+1)-(2x1+1)(2x2-1) (2x1+1)(2x2+1) 2(2x1-2x2) (2x1+1)(2x2+1)
∵x1<x2且f(x)=2x为增函数,
∴2x1 <2x2
又∵(2x1+1)>0;(2x2+1)>0
∴f(x1)-f(x2)<0
故:函数f(x)在x∈(-∞,+∞)上是增函数.

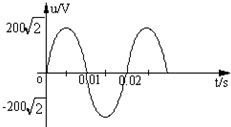
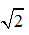 Wb/s
Wb/s V
V