问题
解答题
已知函数f（x）=-x2+2x+c的图象与两坐标轴交于P，Q，R三点。
（Ⅰ）求过P，Q，R三点的圆的方程；
（Ⅱ）试探究，对任意实数c，过P，Q，R三点的圆都经过定点（坐标与c无关）。
答案
解：（Ⅰ）不妨设函数f（x）=-x2+2x+c的图象与x轴交于P，Q两点，与y轴交于R点，
所以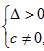
，
即c>-1，且c≠0，
设所求圆的圆心为C（a，b），半径为r，则a=1，
根据点R（0，c）及|CP|=r=|CR|，
得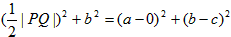
即1+c+b2=1+b2-2bc+c2，
由c≠0，得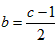
，所以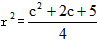
，
故过P，Q，R三点的圆的方程为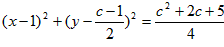
（c>-1，c≠0）；
（Ⅱ）解法一：圆的方程可化为：
x2+y2-2x+y-c（y+1）=0（c>-1，c≠0）
由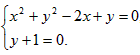
求得定点A（0，-1），B（2，-1），与c无关。
解法二：由于c>-1，且c≠0，不妨令c=1，2分别代入圆的方程
，
求得这两个圆的交点分别足A（0，-1），B（2，-1），
对于任意的c，把点A，B的坐标分别代入圆的方程，等式恒成立，与c无关，故所求的定点是A（0，-1），B（2，-1）。