问题
解答题
已知动圆M与圆C1：(x+4)2+y2=4外求，与圆C2：(x-4)2+y2=100内切，求动圆圆心M 的轨迹方程。
答案
解：设动圆圆心M的半径为R，
则由已知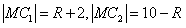
，
所以，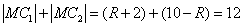
，
又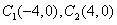
，
所以，
，
根据椭圆定义知，点M的轨迹是以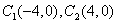
为焦点，长轴为12的椭圆，
因为a=6，c=4，所以，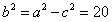
，
所以，点M的轨迹方程是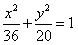
。
搜题请搜索小程序“爱下问搜题”
已知动圆M与圆C1：(x+4)2+y2=4外求，与圆C2：(x-4)2+y2=100内切，求动圆圆心M 的轨迹方程。
解：设动圆圆心M的半径为R，
则由已知，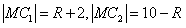
所以，，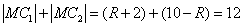
又，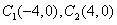
所以，，
根据椭圆定义知，点M的轨迹是以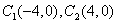为焦点，长轴为12的椭圆，
因为a=6，c=4，所以，，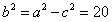
所以，点M的轨迹方程是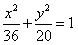。