问题
解答题
已知圆x2+y2+x-6y+3=0与直线x+2y-3=0的两个交点为P、Q,求以PQ为直径的圆的方程.
答案
解:设点P(x1,y1),Q(x2,y2),
则点P、Q的坐标满足方程组x2+y2+x-6y+3=0,x+2y-3=0,
解方程组,得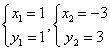 ,
,
即点P(1,1),Q(-3,3),
∴线段PQ的中点坐标为(-1,2),|PQ|=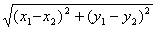 =2
=2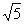 ,
,
故以PQ为直径的圆的方程是(x+1)2+(y-2)2=5。
已知圆x2+y2+x-6y+3=0与直线x+2y-3=0的两个交点为P、Q,求以PQ为直径的圆的方程.
解:设点P(x1,y1),Q(x2,y2),
则点P、Q的坐标满足方程组x2+y2+x-6y+3=0,x+2y-3=0,
解方程组,得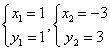 ,
,
即点P(1,1),Q(-3,3),
∴线段PQ的中点坐标为(-1,2),|PQ|=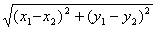 =2
=2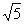 ,
,
故以PQ为直径的圆的方程是(x+1)2+(y-2)2=5。