解：（1）设圆心坐标为（a，b），

则所求圆的方程为，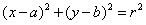

∵圆心在y=-x上，

∴b=-a，                                                               ①

又∵圆过（2，0），（0，-4），

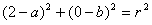∴ ，                               ② 

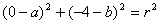   ，                              ③

由①②③联立方程组，可得，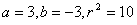

∴所求圆的方程为。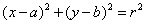

（2） ∵圆与直线x+y-1=0相切，并切于点M（2，-1），

则圆心必在过点M（2，-1）且垂直于x+y-1=0的直线：y=x-3上，

由，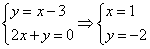

即圆心为C（1，-2），

∴r=，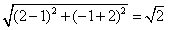

∴所求圆的方程为：。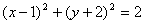

（3）设所求圆的方程为，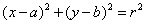

∵圆与坐标轴相切，

∴，

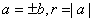又∵圆心(a，b)在直线5x-3y=8上，

∴5a-3b=8，

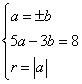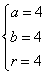由，得或，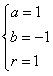

∴所求圆的方程为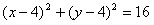：或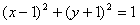。