问题
解答题
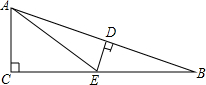
如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,
(1)求证:AE=BE;
(2)求证:∠AEC=2∠B;
(3)求∠B的度数.
答案
(1)证明:∵DE是线段AB的垂直平分线,
∴AE=BE. …(4分)
(注意:若证三角形全等得线段相等给满分)
(2)证明:∵AE=BE,
∴∠B=∠EAD,
∴∠AEC=∠B+∠EAD=2∠B.
(3)设∠B=x°,则∠CAE=4x°
∴4x+x+x+90=180,
∴x=15°.
