问题
解答题
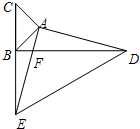
如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,点B、C、E在同一条直线上,AC=AB,AD=AE,且AE与BD交于点F,你能判断出CE与BD的关系吗?请说明理由.
答案
BD=CE,BD⊥CE,理由是:
∵∠DAE=∠BAC=90°,
∴∠CAE=∠BAD,
在△ACE和△ABD中,
,AC=AB ∠CAE=∠BAD AE=AD
∴△ACE≌△ABD(SAS),
∴CE=BD,∠ACE=∠ABD.
在Rt△ABC中,∠ABC+∠ACE=90°,
∴∠ABD+∠ABC=90°,即CD⊥BE.
