问题
解答题
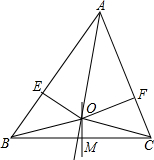
辨析题:在△ABC中,已知AB>AC,求证:AB=AC.
证明:如图,作∠BAC的平分线与边BC的中垂线交于点O,
则OB=OC,再作OE垂直AB于E,OF垂直AC于F,则OE=OF,
∴Rt△BOE≌Rt△COF,
∴BE=CF,①
在Rt△AOE和Rt△AOF中,OE=OF,AO=AO,
∴Rt△AOE≌Rt△AOF
∴AE=AF,②
由①、②得,AB=AC.
上述画图与证明过程中,哪里出错了呢?
这说明我们今后在解题时又要注意什么呢?
在△ABC中,AB>AC,∠BAC的平分线与边BC的中垂线相交于点O,OE垂直AB于点E,那么三条线段AB、AC、BE有何等量关系?请你写出来并加以证明.
答案
图形出现错误,如图所示:
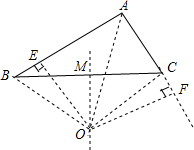
三条线段AB、AC、BE的等量关系为AB=AC+2BE,理由如下:
∵AO为∠BAC的平分线,OE⊥AB,OF⊥AC,
∴OE=OF,
在Rt△AOE和Rt△AOF中,
,OA=OA OE=OF
∴Rt△OEB≌Rt△OFC(HL),
∴AE=AF,
又OM为BC的垂直平分线,
∴OB=OC,
在Rt△OEB和Rt△OFC中,
,OB=OC OE=OF
∴Rt△OEB≌Rt△OFC(HL),
∴BE=CF,
则AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE.
