阅读下文,完成文后各题。
张逸园家传
姚鼐
张逸园君者,讳若瀛,字印沙。君为人慷慨强果,自其少时,里人皆异之矣。君始以诸生为书馆誊录,叙劳授主簿,借补热河巡检。热河今为承德府,君仕时,未设府、县,以巡检统地逾百里。岁为天子巡驻之所,四方民汇居其间,君以严能治办, * * 蠹屏除。留守内监为僧者曰于文焕,君一日行道,见其横肆,立呼至杖之。于是热河内府总管怒,奏君擅杖近御,直隶总督亦劾君。上闻之,顾喜君强毅,不之罪,而以劾君者为非。
其后为良乡知县,顺天府南路同知①。有旗民张达祖,居首辅傅忠勇公门下,始有地数百顷,卖之民矣,久而地值百倍,达祖以故值取赎,构讼,经数官,不敢为民直。君至,傅忠勇颇使人示意君也,君告之以义,必不可,卒以田归民。畿南多回民,久聚为窃盗,不可胜诘。君多布耳目,得其巨魁,或亲捕之,凡半年,获盗百余。盗畏之甚,乃使一回民伪来首云:“有某人至其家,巨盗也。”及捕之至,即自首:“某案己所为盗,有赃在京师礼拜寺②。”君使兵役偕之至礼拜寺,则反与哄斗。至刑部讯,以某案事与此人无与,以君为诬良,议当革职;既而上见君名,疑部议不当,召君,令军机处复问,减君罪,发甘肃以知县用。是时上意颇向君,然卒降黜者,大臣固不助君也。
在甘肃二年,尝为张掖复营兵所夺民渠水利,又以张掖黑河道屡迁,所过之田,为沙砾数百顷,而岁输粮草未除,力请总督除之。时甘肃官相习伪为灾荒请赈,而实侵入其财,自上吏皆以为当然,君独不肯为。其后为者皆败,于是世益推君。
君引疾去甘肃,里居数年。君居里为园,时游之,名之曰逸园,言己不得尽力为国劳而苟逸也,故人以逸园称之。
【注】①同知:官名,清代为知府、知州的佐官。②礼拜寺:又名清真寺,回族穆斯林举行礼拜和宗教活动的场所,兼有传播宗教知识、培养宗教职业者的使命。
小题1:对下列句子中加点词的解释,不正确的一项是(3分)
A.叙劳授主簿,借补热河巡检叙:议叙
B.君一日行道行:行走
C.久聚为窃盗,不可胜诘诘:究办
D.岁输粮草未除输:缴纳小题2:下列句子中,全都直接表现张逸园“慷慨强果”的一组是(3分)
①见其横肆,立呼至杖之 ②君告之以义,必不可 ③盗畏之甚
④君使兵役偕之至礼拜寺 ⑤力请总督除之 ⑥自上吏皆以为当然,君独不肯为
A.①⑤⑥
B.②③④
C.①②⑤
D.②④⑥小题3:下列对原文有关内容的分析和概括,不正确的一项是(3分)
A.张逸园为人慷慨强果,年轻的时候,乡里人就视他为不同寻常的人。在热河巡检任内,他严肃整治,肃
清了 * * 诈邪恶之人。
B.在顺天府良乡任内,张逸园因为整治回民窃盗有方招致陷害,尽管在皇帝的干预下免于处罚,但仍被发配到甘肃降职使用。
C.不经请示就用杖刑处罚做和尚的内监,勇于制止权贵门下的霸道行径,表现了张逸园坚决捍卫正义、敢于得罪权贵的高贵品质。
D.在甘肃,官兵侵占民渠,官员谎报灾情以达到贪污的目的,社会政治的黑暗可见一斑。张逸园退居乡里后,把园子命名为“逸园”,反映了他与现实的不相容。
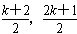 ),
),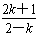 ,
,