问题
解答题
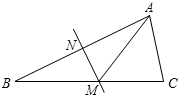
已知：如图，在△ABC中，MN是边AB的中垂线，∠MAC=50°，∠C=3∠B，求∠B的度数．
答案
∵MN是边AB的中垂线，
∴AM=BM，
∴∠BAM=∠B，
设∠B=x，则∠BAM=x，
∵∠C=3∠B，∴∠C=3x，
在△ABC中，由三角形内角和定理，得x+x+3x+50°=180°，
∴x=26°，
即∠B=26°．
搜题请搜索小程序“爱下问搜题”
已知：如图，在△ABC中，MN是边AB的中垂线，∠MAC=50°，∠C=3∠B，求∠B的度数．
∵MN是边AB的中垂线，
∴AM=BM，
∴∠BAM=∠B，
设∠B=x，则∠BAM=x，
∵∠C=3∠B，∴∠C=3x，
在△ABC中，由三角形内角和定理，得x+x+3x+50°=180°，
∴x=26°，
即∠B=26°．