问题
解答题
已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2),求圆心C在l1上且与直线l2相切于点P的圆的方程.
答案
解:设圆心为C(a,b),半径为r,依题意,得b=-4a,
又PC⊥l2,直线l2的斜率k2=-1,
∴过P,C两点的直线的斜率kPC=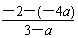 =1,
=1,
解得a=1,b=-4,r=|PC|=2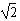 ,
,
故所求圆的方程为(x-1)2+(y+4)2=8。
已知直线l1:4x+y=0,直线l2:x+y-1=0以及l2上一点P(3,-2),求圆心C在l1上且与直线l2相切于点P的圆的方程.
解:设圆心为C(a,b),半径为r,依题意,得b=-4a,
又PC⊥l2,直线l2的斜率k2=-1,
∴过P,C两点的直线的斜率kPC=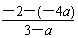 =1,
=1,
解得a=1,b=-4,r=|PC|=2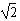 ,
,
故所求圆的方程为(x-1)2+(y+4)2=8。