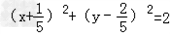问题
解答题
求经过A（0，﹣1）和直线x+y=1相切，且圆心在直线y=﹣2x上的圆的方程．
答案
解：因为圆心在直线y=﹣2x上，设圆心坐标为（a，﹣2a）
设圆的方程为（x﹣a）2+（y+2a）2=r2
圆经过点A（0，﹣1）和直线x+y=1相切，
所以有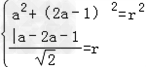
解得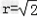
，a=1或
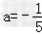
所以圆的方程为（x﹣1）2+（y+2）2=2或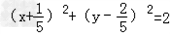
搜题请搜索小程序“爱下问搜题”
求经过A（0，﹣1）和直线x+y=1相切，且圆心在直线y=﹣2x上的圆的方程．
解：因为圆心在直线y=﹣2x上，设圆心坐标为（a，﹣2a）
设圆的方程为（x﹣a）2+（y+2a）2=r2
圆经过点A（0，﹣1）和直线x+y=1相切，
所以有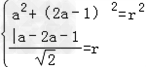
解得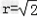，a=1或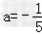
所以圆的方程为（x﹣1）2+（y+2）2=2或