解：(1)设动点为M，其坐标为(x，y)，

当x≠±a时，由条件可得，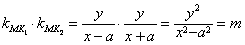

即mx²-y²=ma²(x≠±a)，

又A₁(-a，0)、A₂(a，0)的坐标满足mx²-y²=ma²，

故依题意，曲线C的方程为mx²-y²=ma²，

当m＜-1时，曲线C的方程为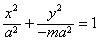，C是焦点在y轴上的椭圆；

当m=-1时，曲线C的方程为x²+y²=a²，C是圆心在原点的圆；

当-1＜m＜0时，曲线C的方程为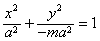，C是焦点在x轴上的椭圆；

当m＞0时，曲线C的方程为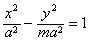，C是焦点在x轴上的双曲线．

(2)由(1)知，当m=-1时，C₁的方程为x²+y²=a²；

当m∈(-1，0)∪(0，+∞)时，C₂的两个焦点分别为，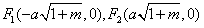

对于给定的m∈(-1，0)∪(0，+∞)，C₁上存在点N(x₀，y₀)(y₀≠0)使得S=|m|a²的充要条件是

，

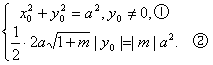由①得0＜|y₀|≤a，由②得，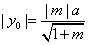

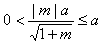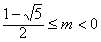当，即，或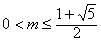时，存在点N，使S=|m|a²；

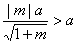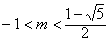当，即，或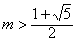时，不存在满足条件的点N；

当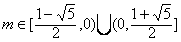时，

由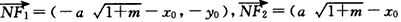，-y₀)，

可得，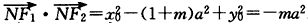

令，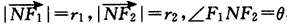

则由，

可得，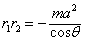

从而，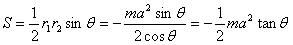

于是由S=|m|a²，可得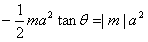，即，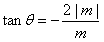

综上可得：当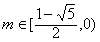时，在C₁上，存在点N，使得S=|m|·a²，且tanF₁NF₂=2；

当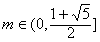时，在C₁上，存在点N，使得S=|m|·a²，且tanF₁NF₂=-2；

当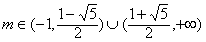时，在C₁上，不存在满足条件的点N．