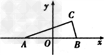
解：以AB所在直线为x轴，AB的中点为坐标原点，建立如图所示的直角坐标系，

则有A（-a，0），B(a，0)，设顶点C(x，y).  

解法一：由△ABC是直角三角形可知|AB|²=|AC|²+|BC|²，

即(2a)²=(x+a)²+y²+(x-a)²+y2，

化简得x²+y²=a²．

依题意可知x≠±a．    

故所求直角顶点C的轨迹方程为x²+y²=a²（x≠±a）．    

解法二：由△ABC是直角三角形可知AC⊥BC，

所以k_AC·k_BC=-1，

则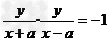(x≠±a)，

化简得直角顶点C的轨迹方程为x²+y²=a²（x≠±a）．    

解法三：由△ABC是直角三角形可知|OC|=|OB|，

所以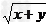=a，

化简得直角顶点C的轨迹方程为x²+y²=a²(x≠±a).