问题
解答题
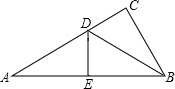
如图，在△ABC中，∠C=90°，DE是AB的垂直平分线，交AC于D，垂足为E，∠ABD：∠ABC=1：2，求∠A的度数．
答案
设∠ABD=x°，
∵∠ABD：∠ABC=1：2，
∴∠ABC=2x°，
∵DE是AB的垂直平分线，
∴AD=BD，
∴∠A=∠ABD=x°，
∵在△ABC中，∠C=90°，
∴∠A+∠ABC=90°，
即x+2x=90，
解得：x=30，
∴∠A=30°．
搜题请搜索小程序“爱下问搜题”