问题
解答题
已知矩形ABCD的两条对角线相交于点M（2，0），AB边所在直线的方程为：x-3y-6=0，点T（-1，1）在AD边所在直线上，
（1）求矩形ABCD外接圆的方程；
（2）求矩形ABCD外接圆中，过点G（1，1）的最短弦EF所在的直线方程。
答案
解：（1）设A点坐标为（x，y），
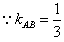且AB⊥AD，
∴
，
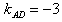又T（-1，1）在AD上，
∴
，
∴
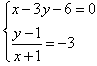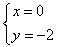，即A点的坐标为（0，-2）。
又∵M点是矩形ABCD两条对角线的交点，
∴M点（2，0）即为矩形ABCD外接圆的圆心，其半径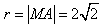
，
∴圆方程为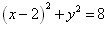
；
（2）当EF⊥MG时，弦BC最短，
，
∴
，
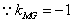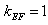所以直线EF的方程为x-y=0。