问题
解答题
已知圆C过点P（1，1）且与圆M：（x+2）2+（y+2）2=r2（r＞0）关于直线x+y+2=0对称，作斜率为1的直线l与圆C交于A，B两点，且点P（1，1）在直线l的左上方，
（1）求圆C的方程；
（2）证明：△PAB的内切圆的圆心在定直线x=1上；
（3）若∠APB=60°，求△PAB的面积。
答案
解：(1)设圆心C（a，b），则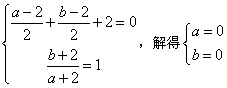
，
∴
，
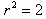∴圆C的方程为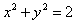
；
（2）设直线AB的方程为：y=x+m，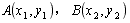
，
由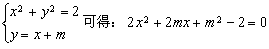
，
∴
，
∴
，
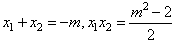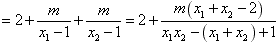
从而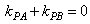
，
因此，∠APB的平分线为垂直于x轴的直线，
又P（1，1），所以△PAB 的内切圆的圆心在直线x=1上。
（3）若∠APB=60°，结合（2）可知：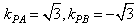
，
直线PA的方程为：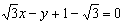
，
圆心O到直线PA的距离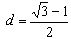
，
∴
，
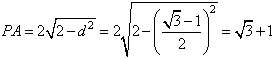同理可得：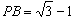
；
∴
。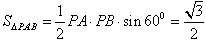