问题
解答题
已知△ABC的顶点A(0,1),AB边上的中线CD所在的直线方程为2x-2y-1=0,AC边上的高BH所在直线的方程为y=0。
(1)求△ABC的顶点B、C的坐标;
(2)若圆M经过不同的三点A、B、P(m,0),且斜率为1的直线与圆M相切于点P,求圆M的方程。
答案
解:(1)AC边上的高BH所在直线的方程为y=0,所以,AC:x=0,
又CD:2x-2y-1=0,所以 ,
,
设B(b,0),则AB的中点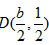 ,代入方程2x-2y-1=0,解得b=2,所以B(2,0);
,代入方程2x-2y-1=0,解得b=2,所以B(2,0);
(2)由A(0,1),B(2,0)可得,圆M的弦AB的中垂线方程为4x-2y-3=0,注意到BP也是圆M的弦,所以,圆心在直线x=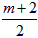 上,设圆心M坐标为
上,设圆心M坐标为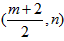 ,
,
因为圆心M在直线上4x-2y-3=0,
所以2m-2n+1=0…………①,
又因为斜率为1的直线与圆M相切于点P,所以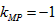 ,即
,即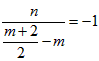 ,
,
整理得 …………②,
…………②,
由①②解得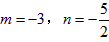 ,
,
所以,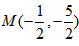 ,半径
,半径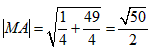 ,
,
所以所求圆方程为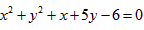 。
。

 尊
尊  珠
珠