问题
解答题
一个圆的圆心在直线x﹣y﹣1=0上，与直线4x+3y+14=0相切，在3x+4y+10=0上截得弦长为6，求圆的方程．
答案
解：由圆心在直线x﹣y﹣1=0上，可设圆心为（a，a﹣1），半径为r，由题意可得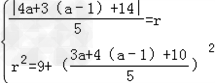
，
经计算得a=2，r=5．
所以所求圆的方程为（x﹣2）2+（y﹣1）2=25
搜题请搜索小程序“爱下问搜题”
一个圆的圆心在直线x﹣y﹣1=0上，与直线4x+3y+14=0相切，在3x+4y+10=0上截得弦长为6，求圆的方程．
解：由圆心在直线x﹣y﹣1=0上，可设圆心为（a，a﹣1），半径为r，由题意可得，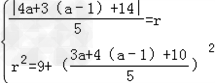
经计算得a=2，r=5．
所以所求圆的方程为（x﹣2）2+（y﹣1）2=25