问题
解答题
证明:线段垂直平分线上的点到这条线段两个端点的距离相等.
答案
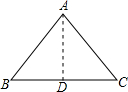
如图所示,当A,D不重合,已知,AD⊥BC,DB=CD.
求证:AB=AC,
证明:∵AD⊥BC,DB=CD.
∴AD=AD,∠ADB=∠ADC,BD=DC,
∴△ADB≌△ADC,
∴AB=AC.
当A,D重合,
D为BC的中点,则BD=DC,
故线段垂直平分线上的点到这条线段两个端点的距离相等.
证明:线段垂直平分线上的点到这条线段两个端点的距离相等.

如图所示,当A,D不重合,已知,AD⊥BC,DB=CD.
求证:AB=AC,
证明:∵AD⊥BC,DB=CD.
∴AD=AD,∠ADB=∠ADC,BD=DC,
∴△ADB≌△ADC,
∴AB=AC.
当A,D重合,
D为BC的中点,则BD=DC,
故线段垂直平分线上的点到这条线段两个端点的距离相等.