问题
解答题
| 如图,在四边形ABCD中,AD∥BC,点E是DC的中点,BE⊥DC,点F在线段BE上,且满足BF=AB,FC=AD.求证: (1)∠A=∠BFC. (2)∠FBC=
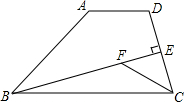 |
答案
证明:(1)连接BD,
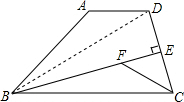
∵点E是DC的中点,BE⊥DC,
∴BE垂直平分DC,
∴BD=BC,
∵在△ABD与△FBC中,
,AB=FB BD=BC AD=FC
∴△ABD≌△FBC(SSS),
∴∠A=∠BFC;
(2)由(1)知△ABD≌△FBC,
∴∠ADB=∠FCB,
∵AD∥BC,
∴∠ADB=∠DBC
∵BD=BC且BE⊥DC,
∴∠FBC=
∠DBC,1 2
∴∠FBC=
∠ADB1 2
即∠FBC=
∠BCF.1 2
