问题
填空题
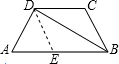
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=2,∠A=60°,BD平分∠ABC,则这个梯形的周长是____.
答案
10
分析:根据平行线的性质推出∠CDB=∠DBA,得出∠CDB=∠CBD,推出DC=BC,过D作DE∥BC交AB于E,推出四边形DEBC是平行四边形,得出DC=BE,DE=BC,∠DEA=∠CBA,证△ADE是等边三角形,求出AE即可.
解:∵DC∥AB,
∴∠CDB=∠DBA,
∵BD平分∠ABC,
∴∠CBD=∠DBA,
∴∠CDB=∠CBD,
∴DC=BC=2cm,
过D作DE∥BC交AB于E,
∵DC∥AB,DE∥BC,
∴四边形DEBC是平行四边形,
∴DC=BE,DE=BC,∠DEA=∠CBA,
∵DC∥AB,AD=BC,
∴∠A=∠CBA=∠DEA=60°,
∴AD=DE,
∴△ADE是等边三角形,
∴AE="AD=2" ,
∴这个梯形的周长是AB+BC+CD+AD="2" +2 + 2 + 2 +2 =10,
故答案为:10.
