问题
选择题
矩形的两条对角线的夹角为60°,这个矩形较短边与对角线的比是( )
A.1∶1
B.1∶2
C.2∶3
D.1∶
答案
答案:B
专题:计算题.
分析:根据矩形的两条对角线的夹角为60°,可以判定△AOB为等边三角形,即可求得AB=AO,在直角△ABC中,已知AC,AB,根据勾股定理即可计算BC的长,进而计算矩形的周长即可解题.
解答:解:
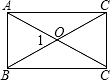
矩形的两条对角线的夹角为∠1=60°,
且矩形对角线相等且互相平分,
∴△AOB为等边三角形,
∴AB=AO= AC,
AC,
故选B.
点评:本题考查了矩形对角线相等且互相平分的性质,等边三角形的判定,勾股定理在直角三角形中的运用,本题中根据勾股定理计算BC的长是解题的关键.
