问题
解答题
如图,在△ABC中,AD平分∠BAC,DE∥AC,EF⊥AD交BC延长线于F.求证:∠FAC=∠B.
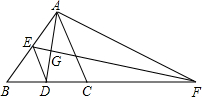
答案
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,

∵DE∥AC,
∴∠EDA=∠CAD,
∴∠EDA=∠EAD,
∴AE=ED,
又∵EF⊥AD,
∴EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
又∵∠FAD=∠CAD+∠FAC,
∠FDA=∠B+∠BAD,
∴∠FAC=∠B.
