两边平方整理得：（|x|-1）²=2y-y²，

化简得（|x|-1）²+（y-1）²=1，

由|x|-1≥0得x≥1或x≤-1，

当x≥1时，方程为（x-1）²+（y-1）²=1，

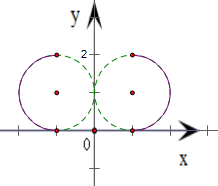
表示圆心为（1，1）且半径为1的圆的右半圆；

当x≤1时，方程为（x+1）²+（y-1）²=1，

表示圆心为（-1，1）且半径为1的圆的右半圆

综上所述，得方程|x|-1=

故选：A