问题
填空题
正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .
答案
15 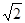 /8
/8
ABCD为正方形,所以BD平分AC
因此A为C关于BD的对称点,BD上任意一点到A与C距离相等
因此PE+PC最小,即PE+PA最小
所以连接A、E,与BD交点即为所求P点
从P作PH垂直BC于H
简单有△EPH∽△EBA,EH:EB=PH:AB
因为BD为正方形对角线,所以∠PBH为45度
△PBH为等腰直角三角形,PH=BH,PB=√2PH
设PH为X,则EH为3-X
(3-X):3=X:5
8X=15
X=15/8
PB=15√2/8
