问题
解答题
若不等式|x﹣a|+|x|＜2没有实数解，求a的取值范围．
答案
解：∵|x﹣a|+|x|＜2，
∴|x﹣a|＜2﹣|x|，
设y1=|x﹣a|，y2=2﹣|x|，
∴y1=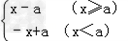
，y2=
，
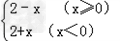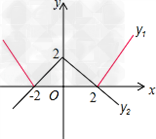
根据原不等式没有实数解，即y1＜y2没有实数解，
从两函数图象可以看出：a≦﹣2或a≧2时，y1的图象在y2的图象下方．
故答案为a≦﹣2或a≧2．
搜题请搜索小程序“爱下问搜题”
若不等式|x﹣a|+|x|＜2没有实数解，求a的取值范围．
解：∵|x﹣a|+|x|＜2，
∴|x﹣a|＜2﹣|x|，
设y1=|x﹣a|，y2=2﹣|x|，
∴y1=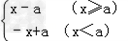，y2=，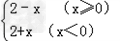
根据原不等式没有实数解，即y1＜y2没有实数解，
从两函数图象可以看出：a≦﹣2或a≧2时，y1的图象在y2的图象下方．
故答案为a≦﹣2或a≧2．