问题
解答题
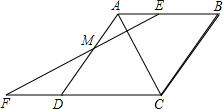
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
(1)求证:AM=DM;
(2)若DF=2,求菱形ABCD的周长.
答案
(1)证明:∵四边形ABCD是菱形,
∴∠BAC=∠DAC.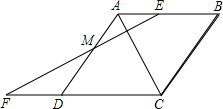
又∵EF⊥AC,
∴AC是EM的垂直平分线,
∴AE=AM,
∵AE=AM=
AB=1 2
AD,1 2
∴AM=DM.
(2)∵AB∥CD,
∴∠AEM=∠F.
又∵∠FMD=∠AME,∠AME=∠AEM,
∴∠FMD=∠F,
∴△DFM是等腰三角形,
∴DF=DM=
AD.1 2
∴AD=4.
∴菱形ABCD的周长是16.
