问题
解答题
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠A=40度.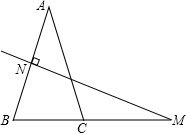
(1)求∠NMB的度数;
(2)如果将(1)中∠A的度数改为70°,其余条件不变,再求∠NMB的度数;
(3)你发现有什么样的规律性,试证明之;
(4)若将(1)中的∠A改为钝角,你对这个规律性的认识是否需要加以修改?
答案
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
(180°-∠A)=1 2
(180°-40°)=70°,1 2
∴∠NMB=90°-∠B=90°-70°=20°;
(2)∵AB=AC,
∴∠B=∠ACB,
∴∠B=
(180°-∠A)=1 2
(180°-70°)=55°,1 2
∴∠NMB=90°-∠B=90°-55°=35°;
(3)规律:∠NMB的度数等于顶角∠A度数的一半,
证明:∵AB=AC,
∴∠B=∠ACB,
∴∠B=
(180°-∠A),1 2
∵∠BNM=90°,
∴∠NMB=90°-∠B=90°-
(180°-∠A)=1 2
∠A,1 2
即∠NMB的度数等于顶角∠A度数的一半;
(4)将(1)中的∠A改为钝角,这个规律不需要修改,
仍有等腰三角形一腰的垂直平分线与底边或底边的延长线相交所成的锐角等于顶角的一半.
