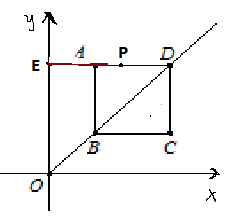
已知正方形ABCD,点B与坐标原点O重合,BC、BA分别在x轴和y轴上,对角线BD在射线OM上,点E在y轴上,OA、OE的长分别是2和6,正方形ABCD以每秒2个单位长度的速度沿射线OM(BD始终在射线OM上)方向移动,同时点P从点C以每秒1个单位长度的速度沿折线CD—DA向点A移动,当一点到达终点时,另一点也停止移动,设移动时间为t秒
小题1:当0≤t≤2时,直接写出点P的坐标(用t的代数式表示).
小题2:当四边形EABO是等腰梯形时,①求t的值;②求证:OA=ED
小题3:是否存在这样的t值,使EP//x轴,若有,求出点P的坐标;若没有,说明理由。
小题1: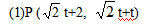
小题2: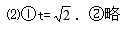
小题3: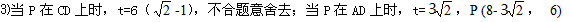
解:(1)如图1, 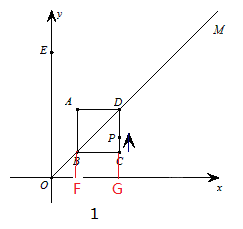 做BF⊥x轴于F,CG⊥x轴于G;
做BF⊥x轴于F,CG⊥x轴于G;
∵当0≤t≤2时点P的横坐标为:BC+OF;而△BOF为等腰直角三角形,且斜边OB=2t;
∴OF=FB=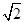 t,OG=OF=FG=
t,OG=OF=FG=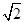 t+2;
t+2;
∵P的纵坐标为PC+CG=FB+CP=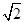 t+t;
t+t;
∴P(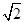 t+2,
t+2, 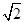 t+t)
t+t)
(2)如图2,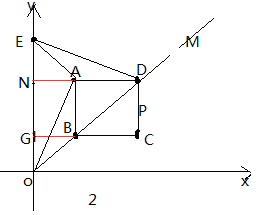
①∵GB=OG=AN=EN=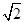 t∴OE=OG+GN+EN=2
t∴OE=OG+GN+EN=2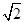 t+2 =6,t=
t+2 =6,t=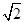
②∵∠OBA=90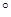 +45
+45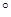 =135
=135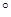 ,∠EAD =180
,∠EAD =180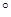 -45
-45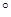 =135
=135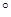 ;
;
∴∠OBA=∠EAD,又AB=AD,AE=OB,∴△OBA △EAD(SAS)
△EAD(SAS)
∴OA=ED
(3)当P在CD上时,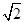 t+t=6,
t+t=6,
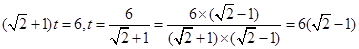 ,不符合题意舍去;
,不符合题意舍去;
当P在AD上时,E在直线AD上,且ED=OE=6,
∴OD=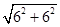 =6
=6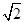 =2t,t=3
=2t,t=3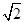 ;
;
此时P的横坐标为DE-PD,而PD=t-2=3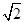 -2,∴DE-PD=8-3
-2,∴DE-PD=8-3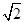 ;
;
∴P(8-3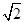 ,6)
,6)