已知函数f(x)=
(1)若函数f(x)在区间[2,+∞)上是单调递增函数,试求实数a的取值范围; (2)当a=2时,求证:1-
(3)求证:
|
(1)因为f ′(x)=
,若函数f(x)在区间[2,+∞)上是单调递增函数,则f′(x)≥0恒成立,即a≥a(x-1)-1 (x-1)2
恒成立,所以a≥(1 x-1
)max.1 x-1
又x∈[2,+∞),则0<
≤1,所以a≥1.1 x-1
(2)当a=2时,由(Ⅰ)知函数f(x)=
+2ln(x-1)在[2,+∞)上是增函数,2-x x-1
所以当x>2时,f(x)>f(2),即
+2ln(x-1)>0,则2ln(x-1)>2-x x-1
=1-x-2 x-1
.1 x-1
令g(x)=2x-4-2ln(x-1),则有g′(x)=2-
=2 x-1
,2(x-2) x-1
当x∈(2,+∞)时,有g′(x)>0,
因此g(x)=2x-4-2ln(x-1)在(2,+∞)上是增函数,所以有g(x)>g(2)=0,
即可得到2x-4>2ln(x-1).
综上有1-
<2ln(x-1)<2x-4(x>2).1 x-1
(3)在(2)的结论中令x-1=
,则t+1 t
<2ln1 t+1
<2•t+1 t
,1 t
取t=1,2,…,n-1,(n∈N*,n≥2)时,得到(n-1)个不等式,将所得各不等式相加得,
+1 2
+…+1 3
<2(ln1 n
+ln2 1
+…+ln3 2
)<2(1+n n-1
+…+1 2
),1 n-1
所以
+1 2
+…+1 3
<2lnn<2(1+1 n
+…+1 2
),1 n-1
即
+1 4
+…+1 6
<lnn<1+1 2n
+…+1 2
(n∈N*且n≥2)1 n-1

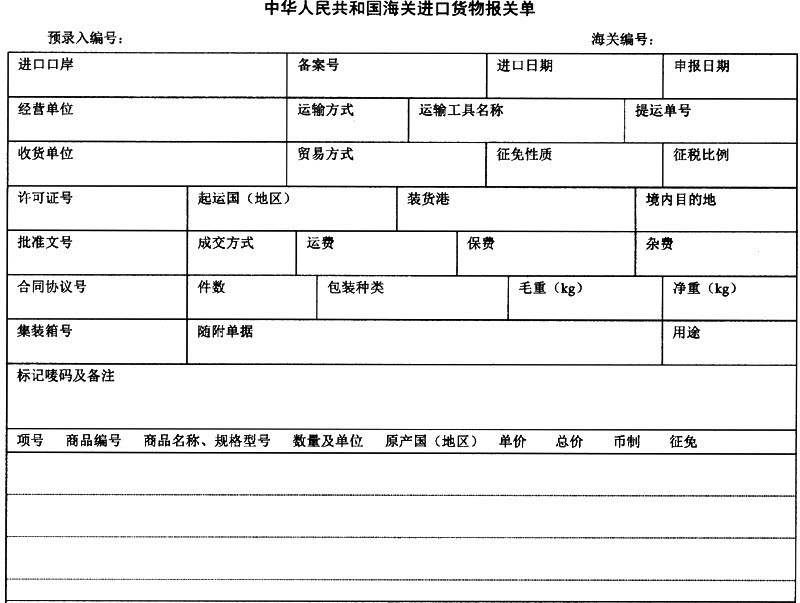
 浙江浙海服装进出口公司(3313910194)在对口合同项下进口蓝湿牛皮,委托浙江嘉宁皮革有限公司(3313920237)加工牛皮沙发革。承运船舶在帕腊纳瓜港装货启运,航经大阪,又泊停釜山港转“HANSA STAVANGER”号轮HV300W航次(提单号:HS03D8765),于2003年7月30日抵吴淞口岸申报进境。经营单位委托上海某货运代理公司持C29083100693号手册和310200103036124号入境货物通关单(代码:A)于次日向海关申报货物进口。该货物法定计量单位为:kg,海运费、港杂费合计1500美元,保险费为140美元。
浙江浙海服装进出口公司(3313910194)在对口合同项下进口蓝湿牛皮,委托浙江嘉宁皮革有限公司(3313920237)加工牛皮沙发革。承运船舶在帕腊纳瓜港装货启运,航经大阪,又泊停釜山港转“HANSA STAVANGER”号轮HV300W航次(提单号:HS03D8765),于2003年7月30日抵吴淞口岸申报进境。经营单位委托上海某货运代理公司持C29083100693号手册和310200103036124号入境货物通关单(代码:A)于次日向海关申报货物进口。该货物法定计量单位为:kg,海运费、港杂费合计1500美元,保险费为140美元。

