问题
解答题
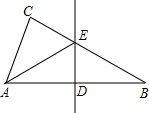
如图,在ABC中,∠C=90°,DE垂直平分AB,分别交AB,BC于D,E.
(1)若∠CAE=∠B+30°,求∠B的大小;
(2)若AC=3,AB=5,求△AEB的周长.
答案
(1)∵DE垂直平分AB,
∴AE=BE,
∴∠B=∠BAE,
∴∠CEA=∠B+∠BAE=2∠B,
在△ACE中,∠CAE+∠CEA=∠B+30°+2∠B=90°,
解得∠B=20°;
(2)由勾股定理得,BC=
=AB2-AC2
=4,52-32
设AE=BE=x,则CE=4-x,
在Rt△ACE中,AC2+CE2=AE2,
即32+(4-x)2=x2,
解得x=
,25 8
∴△AEB的周长=
×2+5=11.25.25 8
