联想三角形外心的概念，我们可引入如下概念．定义：到三角形的两

问题解答题

联想三角形外心的概念，我们可引入如下概念．
定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心．
举例：如图1，若PA=PB，则点P为△ABC的准外心．
应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD=

AB，求∠APB的度数．
探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长．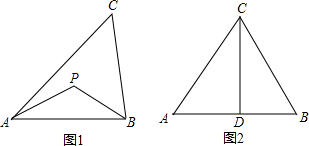

答案

应用：①若PB=PC，连接PB，则∠PCB=∠PBC，

∵CD为等边三角形的高，

∴AD=BD，∠PCB=30°，

∴∠PBD=∠PBC=30°，

∴PD=

DB=

AB，

与已知PD=

AB矛盾，∴PB≠PC，

②若PA=PC，连接PA，同理可得PA≠PC，

③若PA=PB，由PD=

AB，得PD=BD，

∴∠APD=45°，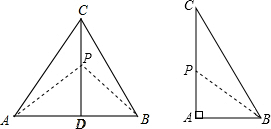

故∠APB=90°；

探究：∵BC=5，AB=3，

∴AC=

BC2-AB2

52-32

=4，

①若PB=PC，设PA=x，则x²+3²=（4-x）²，

∴x=

，即PA=

，

②若PA=PC，则PA=2，

③若PA=PB，由图知，在Rt△PAB中，不可能．

故PA=2或

．