问题
解答题
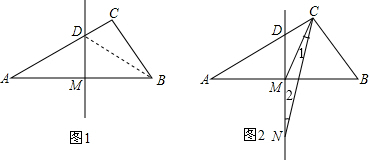
如图1,已知△ABC中,BC=3,AC=4,AB=5,直线MD是AB的垂直平分线,分别交AB、AC于M、D点.
(1)求线段DC的长度;
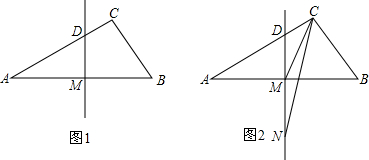
(2)如图2,连接CM,作∠ACB的平分线交DM于N.求证:CM=MN.
答案
(1)如图,连接BD,∵MD是AB的垂直平分线,
∴AD=BD,
设DC=x,则BD=AD=4-x,
在△ABC中,AC2+BC2=42+32=25=AB2,
∴∠C=90°,
在Rt△BCD中,DC2+BC2=BD2,
即x2+32=(4-x)2,
解得x=
,7 8
即DC的长为
;7 8
(2)证明:∵M为AB的中点,△ABC是直角三角形,
∴BM=MC,
∴∠B=∠BCM,
∵CN是∠ACB的平分线,
∴∠BCN=45°,
∴∠B=45°+∠1,
在四边形BCDM中,∠B+90°+∠MDC+90°=360°,
∴∠MDC+∠B=180°,
在△CDN中,∠MDC+45°+∠2=180°,
∴∠MDC=135°-∠2,
∴135°-∠2+45°+∠1=180°,
∴∠1=∠2,
∴CM=MN.