问题
填空题
．已知：正方形ABCD内接于⊙O，点P是⊙O上不同于点B、C的任意一点，则∠BPC的度数是________．
答案
45°或135°
分析：连接BD，则BD是直径，△BCD是等腰直角三角形，即∠BDC=45°，根据圆周角定理即可证∠BPC=∠BDC=45°，进而利用P点位置不同得出答案．
解答：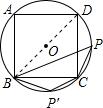
解：连接BD，
则BD是直径，
∴△BCD是等腰直角三角形，
∴∠BDC=45°，
∴∠BPC=∠BDC=45°．
如图所示：
∠BP′C+∠P=180°，
∴∠BP′C=135°．
故答案为：45°或135°．
