问题
解答题
如图,在四边形ABCD中,AD∥BC,对角线AC的中点为O,过点O作AC的垂线分别与AD、BC相交于点E、F,连接AF.求证:AE=AF.

答案
证明:连接CE,
∵EF是线段AC的垂直平分线,
∴AE=CE,OA=OC,
∵AE∥BC,
∴∠ACB=∠DAC,
在△AOE与△COF中,
∵
,∠ACB=∠DAC OA=OC ∠AOE=∠COF
∴△AOE≌△COF,
∴AE=CF,
∴四边形AFCE是平行四边形,
∵AE=CE,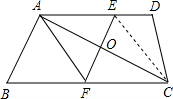
∴四边形AFCE是菱形,
∴AE=AF.
另法:∵AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∵
,∠OAE=∠OCF OA=OC ∠AOE=∠COF
∴△AOE≌△COF﹙ASA﹚,
∴OE=OF,
∴AC垂直平分EF,
∴AE=AF.
