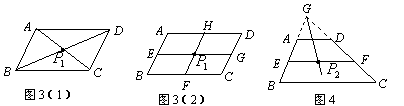问题
探究题
定义:到凸四边形一组对边距离相等,到另一组对边距离也相等的点叫凸四边形的准内点。如图1,PH=PJ ,PI=PG ,则点P就是四边形ABCD的准内点。
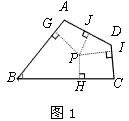
(1)如图2,∠AFD与∠DEC的角平分线FP、EP 相交于点P
求证:点P是四边形ABCD 的准内点;
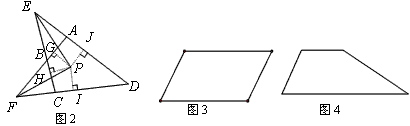
(2)分别画出图3平行四边形和图4梯形的准内点。(作图工具不限,不写作法,但要有必要的说明)
(3)判断下列命题的真假,在括号内填“真”或“假”。
①任意凸四边形一定存在准内点。( )
②任意凸四边形一定只有一个准内点。( )
③若P是任意凸四边形ABCD的准内点,则PA+PB=PC+PD或PA+PC=PB+PD。( )
答案
解:(1)如图2,过点P作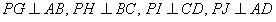 | |
∵EP平分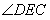 ,∴ ,∴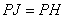 | |
同理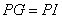 | |
| ∴P是四边形ABCD的准内点。 | |
| (2) | 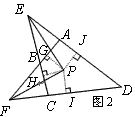 |