问题
解答题
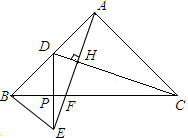
如图,在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,点D是AB的中点,AF⊥CD于H交BC于F,BE∥AC交AF的延长线于E.求证:BC垂直且平分DE.
答案
证明:在△ADC中,∠DAH+∠ADH=90°,∠ACH+∠ADH=90°,
∴∠DAH=∠DCA,
∵∠BAC=90°,BE∥AC,
∴∠CAD=∠ABE=90°.
又∵AB=CA,
∴在△ABE与△CAD中,
∠DAH=∠DCA ∠CAD=∠ABE AB=AC
∴△ABE≌△CAD(ASA),
∴AD=BE,
又∵AD=BD,
∴BD=BE,
在Rt△ABC中,∠ACB=45°,∠BAC=90°,AB=AC,
故∠ABC=45°.
∵BE∥AC,
∴∠EBD=90°,∠EBF=90°-45°=45°,
∴△DBP≌△EBP(SAS),
∴DP=EP,
即可得出BC垂直且平分DE.
