问题
问答题
设f(x)在区间[0,1]上连续,在(0,1)内可导,且f(0)=f(1)=0,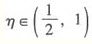 ,试证:
,试证:
对任意实数λ,必存在ξ∈(0,η),使得f’(ξ)-λ[f(ξ)-ξ]=1。
答案
参考答案:
引入辅助函数,由原函数法将所需证明的等式中的ξ改写为x,
有f’(x)-λ[f(x)-x]=1,且f’(x)-λf(x)=1-λx.
由一阶线性非齐次微分方程的通解公式得:
f(x)=e∫λx{C+∫e-∫λdx·(1-λx)dx}=eλx{C+∫e-λx(1-λx)dx}
=eλx{C+∫e-λxdx-∫xe-λxdx}=eλx{C+xe-λx}==Ceλx+x,
所以[f(x)-x]e-λx=C,至此可令辅助函数为g(x)=[f(x)-x]e-λx=-φ(x)e-λx,
由已知条件及(Ⅰ)中结论,知g(x)也是连续函数,
且g(0)=[f(0)-0]e0=0,g(η)=-φ(η)e-λη=0.
由罗尔定理知存在一点ξ∈(0,η),使得g’(ξ)=0,
又g’(x)=-λe-λx[f(x)-x]+e-λx[f’(x)-1],
所以-λ[f(ξ)-ξ]+f’(ξ)-1=0
此即f’(ξ)-λ[f(ξ)-ξ]=1.证毕.
解析:
[考点] 介值定理、罗尔定理
