问题
问答题
设A为3阶矩阵,α1,α2为A的分别属于特征值-1、1的特征向量,向量α3满足Aα3=α2+α3,
证明α1,α2,α3线性无关。
答案
参考答案:
假设α1,α2,α3线性相关,则α3可由α1,α2线性表出,可设α3=k1α1+k2α2,其中k1,k2不全为0,
否则由等式Aα3=α2+α3得到α2=0,不符合题设.
因为α1,α2为矩阵A的分别属于特征值-1,1的特征向量,所以Aα1=-α1,Aα2=α2,
则Aα3=A(k1α1+k2α2)=-k1α1+k2α2=α2+k1α1+k2α2.
等式中α1,α2的对应系数相等,即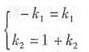
显然此方程组无解,故假设不成立,从而可知α1,α2,α3线性无关.

