参考答案：B

解析：

[考点] 线性表示

由题设，β可由向量组α₁，α₂，…，α_m线性表示，

则存在一组数k₁，k₂，…，k_m，使β=k₁α₁+k₂α₂+…+k_mα_m，

但是β不能由α₁，α₂，…，α_m-1线性表示，从而k_m≠0，

因此，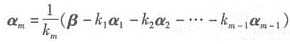

即α_m可由(Ⅱ)α₁，α₂，…，α_m-1，β，线性表示，所以(A)、(D)不正确．

若α_m能由向量组(Ⅰ)线性表示，则存在另一组数λ₁，λ₂，…，λ_m-1，

使得α_m=λ₁α₁+λ₂α₂+…+λ_m-1α_m-1，

从而β=k₁α₁+…+k_m-1α_m-1+k_m[λ₁α₁+λ₂α₂+…+λ_m-1α_m-1]

=(k₁+k_mλ₁)α₁+(α₂+k_mλ₂)α₂+…+(k_m-1+k_mλ_m-1)α_m-1，

这与前述已知矛盾，所以α_m不能由向量组(Ⅰ)线性表示，综上，选(B)．