问题
解答题
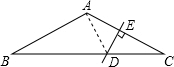
如图,在等腰△ABC中,∠BAC=120°,DE是AC的垂直平分线,DE=1cm,求BD的长.

答案
如图,连接AD,
∵等腰△ABC中,∠BAC=120°,
∴∠B=∠C=
(180°-120°)=30°,1 2
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠DAC=∠C=30°,
∴∠BAD=∠BAC-∠DAC=120°-30°=90°,
在Rt△CDE中,∵DE=1cm,
∴CD=2DE=2cm,
在Rt△ABD中,BD=2AD=2CD=2×2=4cm.