问题
解答题
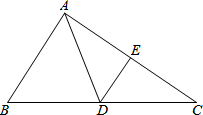
如图,在△ABC中,DE是AC的垂直平分线,AE=6,△ABD的周长为24.
(1)求△ABC的周长;
(2)如果AB∥DE,求△ABC的面积.
答案
(1)∵DE是AC的垂直平分线,
∴AD=CD,AE=CE=6,
∴AC=12.
∵△ABD的周长为24,
∴AB+BD+AC=AB+BD+CD=AB+BC=24,
∴△ABC的周长为:AB+BC+AC=36;
(2)∵AB∥DE,DE⊥AC,
∴AB⊥AC,
设AB=x,则BC=24-x,
在Rt△ABC中,AB2+AC2=BC2,
∴x2+122=(24-x)2,
解得:x=9,
∴S△ABC=
AB•AC=54.1 2
