（1）证明：在平面直角坐标系xOy内作单位圆O，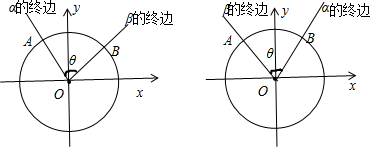

以Ox为始边作角α，β，它们的终边与单位圆O的交点分别为A，B．

则

OA

=（cosα，sinα），

OB

=(cosβ，sinβ)．

则

OA

•

OB

=cosαcosβ+sinαsinβ．

设

OA

与

OB

的夹角为θ，则

OA

•

OB

=|

OA

||

OB

|cosθ=cosθ=cosαcosβ+sinαsinβ．

另一方面，由α=2kπ+β+θ，或α=2kπ+β-θ．

∴α-β=2kπ±θ，k∈Z．

∴cos（α-β）=cosθ．

∴cos（α-β）=cosαcosβ+sinαsinβ．

（2）∵0＜α＜

π

2

，cos(

π

4

+α)=

1

3

，∴

π

4

＜α+

π

4

＜

π

2

，∴sin(α+

π

4

)=

1-cos2(α+ π 4 )

=

2 2

3

．

∵-

π

2

＜β＜0，∴

π

4

＜

π

4

-β＜

3π

4

，∵cos(

π

4

-

β

2

)=

3

3

，∴sin(

π

4

-

β

2

)=

1-cos2( π 4 - β 2 )

=

6

3

．

∴cos(α+

β

2

)=cos[(

π

4

+α)-(

π

4

-

β

2

)]=cos(

π

4

+α)cos(

π

4

-

β

2

)+sin(

π

4

+α)sin(

π

4

-

β

2

)

=

1

3

×

3

3

+

2 2

3

×

6

3

=

5 3

9

．