问题
解答题
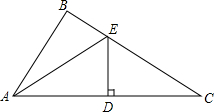
已知D是Rt△ABC斜边AC的中点,DE⊥AC交BC于E,且∠EAB:∠BAC=2:5,求∠ACB的度数.
答案
∵∠EAB:∠BAC=2:5,
∴设∠EAB=2x,则∠BAC=5x,∠EAC=3x,
∵D是Rt△ABC斜边AC的中点,DE⊥AC,
∴AE=CE,
∴∠ACB=∠EAC=3x,
∵∠ACB+∠BAC=90°,即5x+3x=90°,解得x=
,45° 4
∴∠ACB=3×
=33.75°.45° 4
