问题
解答题
如图，在△ABC中，∠C=90°，AB的垂直平分线DE，分别交BC、AB于点D、E，AD平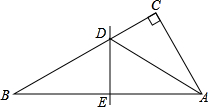
分∠BAC．
（1）写出图中相等的线段，并说明相等的理由．（写出三组，即可得满分）
（2）试判断∠CAD与∠B的大小关系，并推理说明你的判断结论．
答案
（1）∵AB的垂直平分线DE，分别交BC、AB于点D、E，
∴AE=BE（线段垂直平分线定义），
AD=BD（线段垂直平分线上的点到线段两个端点的距离相等）．
∵AD平分∠BAC，DE⊥AB，∠C=90°，
∴CD=ED（角平分线上的点到角两边的距离相等）．
∵AE=
，AC=AD2-DE2
，AD2-CD2
∴AE=AC．
（2）∠CAD=∠B．理由如下：
∵AD=BD，
∴∠BAD=∠B．
又AD平分∠BAC，
∴∠CAD=∠B．