(解法1)因为40°＝30°＋10°，于是原式＝sin²10°＋cos²(30°＋10°)＋sin10°cos(30°＋10°)＝sin²10°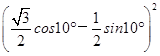＋＋sin10°·(cos10°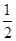－sin10°)＝

(sin²10°＋cos²10°)＝.

(解法2)设x＝sin²10°＋cos²40°＋sin10°cos40°，y＝cos²10°＋sin²40°＋cos10°sin40°.则x＋y＝1＋1＋sin10°cos40°＋cos10°sin40°＝2＋sin50°＝2＋cos40°，x－y＝cos80°－cos20°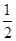－＝－sin50°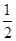－＝－cos40°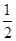－.因此2x＝，故x＝